裂纹偏折是工程实践中无法避免的力学现象，是断裂力学经典问题之一。裂纹可能由于动态裂纹扩展、结构非均匀性、局部应力状态变化等因素导致偏折。经过多年攻关，中科院力学所非线性力学国家重点实验室科研人员在偏折裂纹尖端应力场的求解方面取得突破。该研究成果近期以“An analytical solution to the stress fields of kinked cracks”为题发表在国际权威期刊J. Mech. Phys. Solids上。 

　　通过利用Schwartz-Christoffel变换和Muskhelishvili复势方法，该研究小组求解获得了新复平面上的对应应力函数，并以此为基础求解得到了任意几何尺寸的偏折裂纹尖端应力场（见图一理论与数值结果对照）。以往断裂力学泰斗James Rice等基于摄动方法, John Hutchinson等基于T-应力项叠加的求解方法均仅适用于微小偏转裂纹。该小组的方法突破了偏折裂纹的长度限制，建立了任意长度偏折裂纹尖端应力场弹性解的通用求解方案；该方法同时可推广至多次裂纹偏折的弹性场求解。该研究成果为裂纹偏折行为和裂纹网络的形成机制提供了基础工具。 

　　中科院力学所博士研究生刘卓尔为论文第一作者，魏宇杰研究员为论文通讯作者。该研究得到国家自然科学基金基础科学中心“非线性力学中的多尺度问题”项目（No.11988102），以及中国科学院战略先导项目（XDB22020200）的支持。 

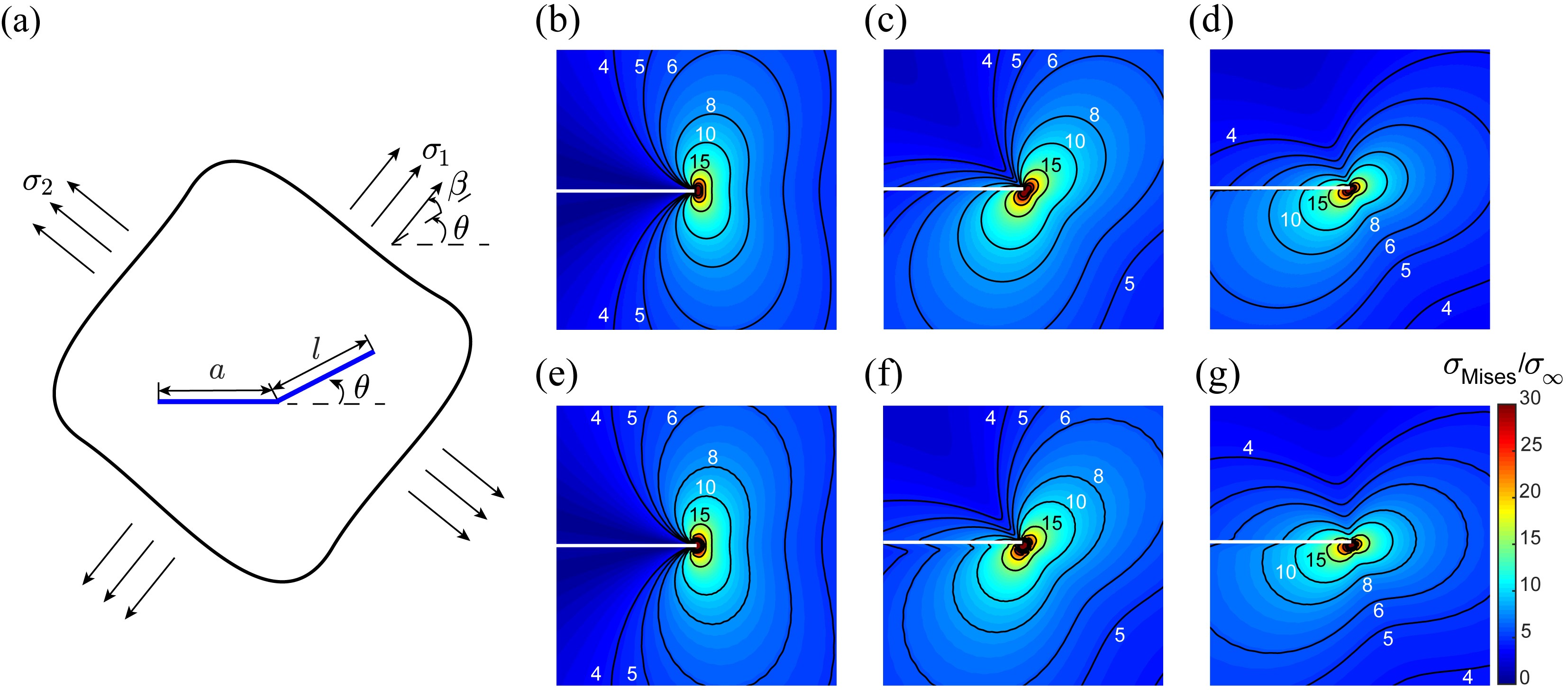
　　图：二维裂纹偏折问题的几何及加载参数以及单轴加载下不同转折角θ对应的裂纹尖端应力场 

　　 论文链接：https://doi.org/10.1016/j.jmps.2021.104619