

力学所提出异质性介质中反常扩散非高斯性的预测和分析新方法
非高斯性是描述复杂系统的特殊行为和统计规律的重要指标。阐明生物复杂流体中纳米颗粒反常扩散的非高斯性根源及规律,对于建立细胞中动力学和结构异质性与功能的关联及研究纳米药物递送的扩散机理有重要意义。力学所非线性力学国家重点实验室微纳米流体力学团队总结以往复杂流体中反常扩散规律,揭示非高斯扩散力学内涵及探索异质性复杂环境的非高斯指标的新进展。该成果最近以“Deciphering non-Gaussianity of diffusion based on the evolution of diffusivity”为题发表于Phys Rev Research (2024, 6, 023014)。
近来,在复杂流体中纳米颗粒反常扩散的研究中,非高斯性逐渐取代非菲克性(或非布朗性)成为新研究前沿。尤其是所谓“菲克非高斯”(Fickian yet non-Gaussian)特征在复杂流体、生物系统乃至玻璃态材料中的颗粒扩散中被广泛观察到,使得非高斯性成为关联该系统反常动力学行为的重要参数,其定量表征及所涵盖的力学、物理作用规律成为关键。
研究团队巧妙地利用热泳微流控芯片建立可控的温度梯度以模拟不同异质性环境(图1),可由此定量研究纳米颗粒在其中扩散的非高斯性与异质性的关联。本研究在微流控实验揭示不同异质性环境中扩散非高斯性规律的基础上,基于diffusing diffusivity模型提出了在扩散系数的统计空间内基于其时空演化预测非高斯性并描述非高斯性变化的新方法,为理解动力学或结构异质性与非高斯性的关联提供了新思路。研究发现,非高斯系数的渐进值可以由扩散系数统计分布的类型和范围决定(图2),一方面为预测不同系统中的非高斯性提供了方法,另一方面为已知非高斯统计特征的条件下逆向重构异质性环境迈出了重要一步,可为当前建立细胞扩散谱的研究提供了力学内涵。研究提出了以等效无量纲Péclet数来刻画非高斯性随时间变化的(图3),由此可解释不同复杂系统中非高斯性随时间的增长或减弱与动力学异质性的时空演化的关联。研究还通过对贝叶斯条件概率统计做Laplace近似,回应了当前研究中关于非高斯概率分布尾部形状函数的争议(图4)。
力学所郑旭副研究员、纳米中心施兴华研究员为论文共同通讯作者。本研究得到了国家自然科学基金、重点研发项目(2022YFF0503504)及中国科学院相关项目的支持。
论文链接:https://doi.org/10.1103/PhysRevResearch.6.023014

图1. 基于热泳微流控芯片建立可控温度梯度模拟不同异质性环境,并在垂直于温度梯度方向测量非高斯扩散,建立非高斯性与异质性的关联

图2. 异质性决定扩散系数统计分布的类型及范围(左),非高斯系数α的短时间渐进值可由扩散系数统计分布决定,长时间渐进值满足1/t的标度率(右)
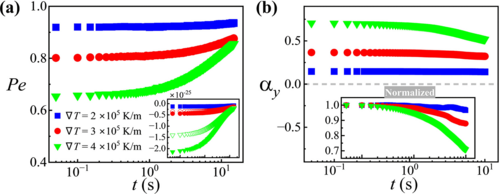
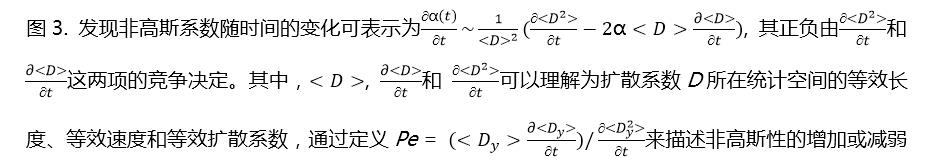
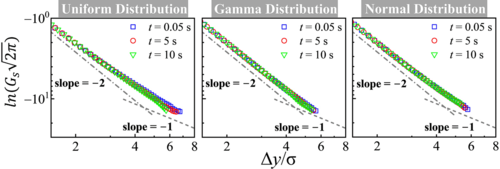
图4. 通过贝叶斯条件概率的Laplace近似,发现不同扩散系数分布的非高斯尾部均会随时间增长趋近于exp(-y2/4Dt),而非以往研究认为的指数型exp(-y/4Dt)
附件下载: