编者按：中国科学院力学研究所的张星研究员团队近期在生物推进尾迹的自发对称性破缺研究方面取得了进展，相关成果发表在国际顶级刊物Physics of Fluids。该项研究得到国家自然科学基金面上项目和中国科学院战略性先导科技专项的支持。

仿水母式推进尾迹演化：理解力学中对称与不对称的美

张星   张治愚

当我们看到自然界中游动和飞行的动物时（参见图1），不禁会问这样一个问题：它们是靠什么来推动自己在空气或水中前行的呢？或者，用力学的术语来说，生物推进的机理是什么？长期以来，流体力学家们一直在研究这个问题。力学研究所的张星研究员团队近期在这个领域取得了进展，他们是从仿水母式推进“尾迹的对称破缺不稳定性”这个视角来进行探讨的。

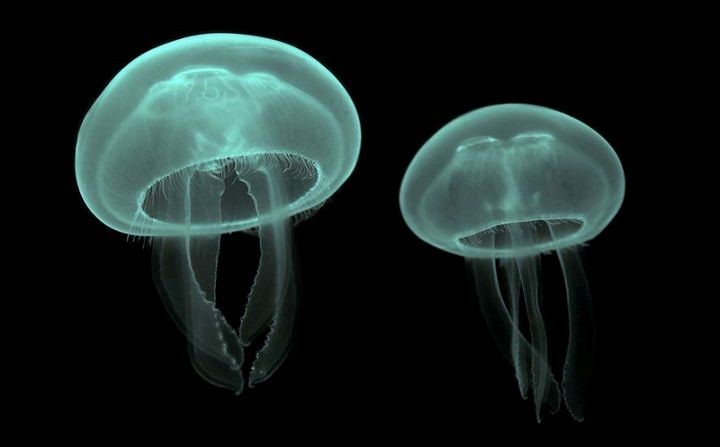
（a）

（b）

（c）

图1 自然界中动物游动与飞行：（a）前进中的水母；（b）并排游动的鱼；（c）双翅打开的昆虫 （图片来源：网络）

这里，我们遇到了好几个力学术语：尾迹，对称破缺，不稳定性，等等。先说明一下“尾迹”的概念。尾迹有时也被称作“尾流”或“尾涡”，是指流体中运动物体后面的旋涡流，可以把它比喻为物体在流体中运动时留下的“足印”。分析尾迹可以反推出物体的受力与运动状态。钝体绕流的尾迹为阻力型，它的速度剖面U/U_∞ 呈亏损型；生物/仿生推进（如鱼游和扑翼）产生的尾迹一般为推力型，它的速度剖面U/U_∞ 呈射流型（参见图2）。

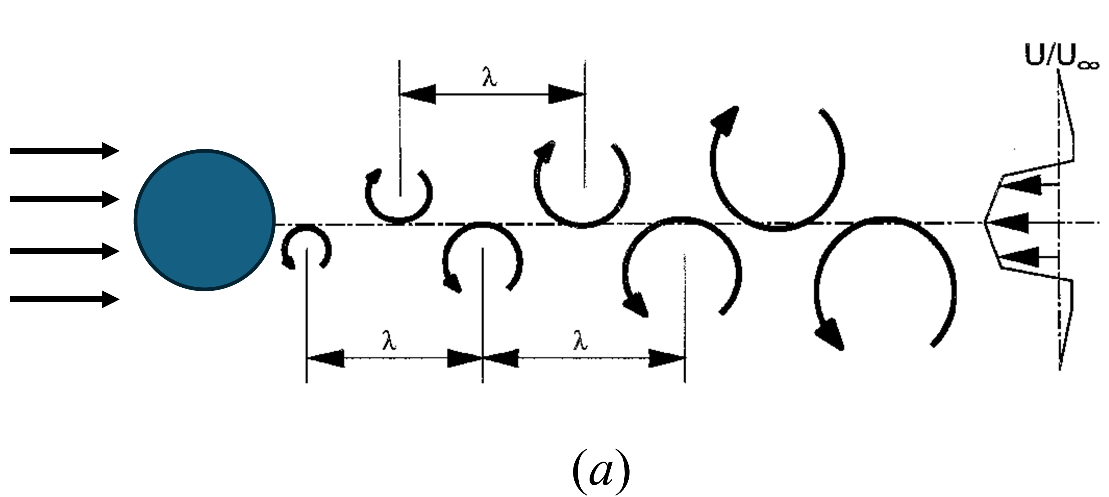
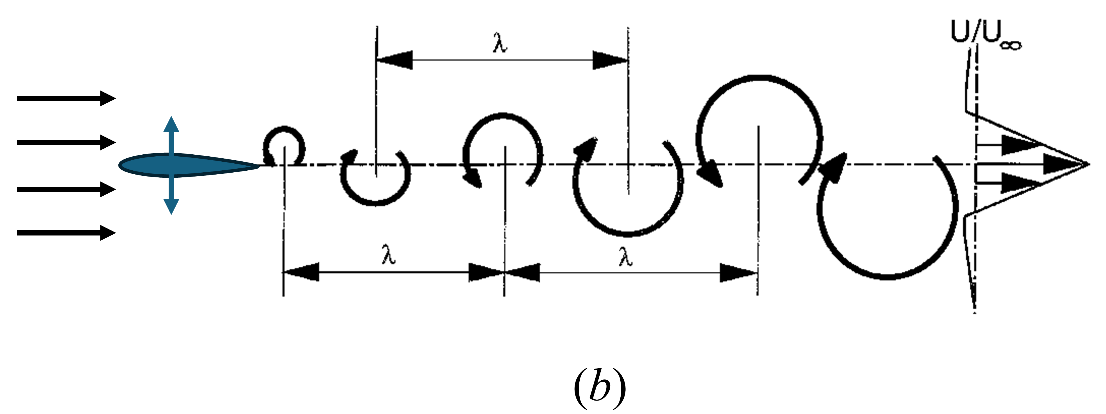
图2 两种典型尾迹及其平均速度剖面：(a) 钝体绕流的阻力型尾迹；(b) 运动扑翼的推力型尾迹（图片来源：参考文献[1]）

再来说明一下“对称性”概念。对称性在力学问题上扮演着重要的角色，这里图3所示的是三种常见的对称性：镜面反射对称性，轴对称性和时空对称性。其中图3c中的时空对称性可以这样来理解：单摆的当前状态（时刻t₀）与半个周期后（时刻t₀+T/2）的状态呈现镜面反射对称。

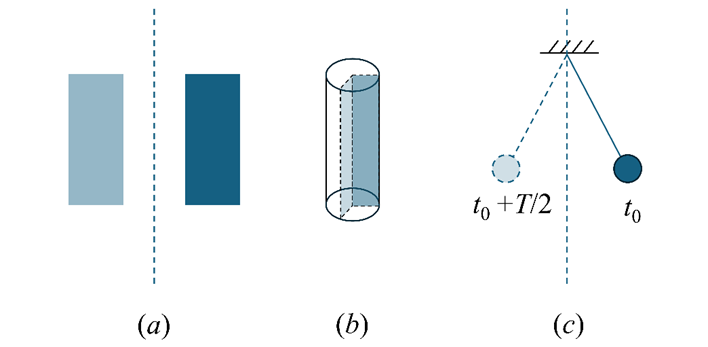
图3 几种常见的对称性：(a) 镜面反射对称性；(b) 轴对称性；(c) 时空对称性（图片来源：作者自绘）

最后说明一下什么是“自发对称破缺不稳定性”。它的发生机理可以这样理解：一个原本具有对称性的系统在受到来自外界的破坏对称性的微小扰动时，扰动会自发地被放大，从而导致系统的对称性明显下降。对称破缺是一个引人入胜的现象，在流体力学中处处都有它的身影。绕流问题中尾迹的类型发生转变时经常伴随着这种现象的出现。下面给出两个经典的例子：（1）当雷诺数（即惯性力与粘性力之比）超过临界值时（约为47左右），圆柱绕流尾迹的空间对称性就无法继续维持。绕流由定常流动演化为具有时空对称性的周期性流动（人们称之为“卡门涡街”）[2][3]（参见图4a）。（2）在某个雷诺数和斯特劳哈尔数（以来流速度和弦长为特征量的无量纲扑动频率）的范围内，扑翼的尾迹（人们称之为“反卡门涡街”）则会失去原有的时空对称性，发生向上方（或下方）一侧的偏转[1][4]（参见图4b）。在图4中，白色和黑色分别表示逆时针和顺时针旋转的旋涡，而且在这个位置处涡量绝对值相对较大。

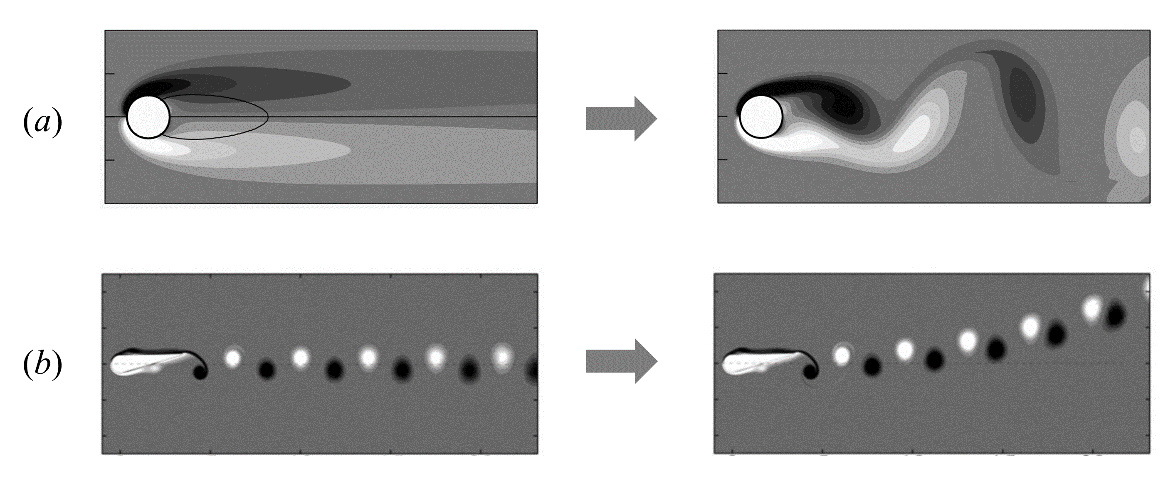
图4 尾迹自发对称破缺的实例：(a) 圆柱绕流尾迹的转变；(b) 扑翼反卡门涡街的转变（图片来源：参考文献[2][4]）

上面讨论的是单个物体的尾迹问题，如果流动系统包含多个物体，那么每个物体的下游都有尾迹，多个物体平行尾迹之间的相互作用便成为了一个更为复杂的流体力学问题。在不同的雷诺数和物体间距范围内，尾迹可能呈现出完全不同的特征。特别是，在来流条件和几何外形完全对称时，尾迹也会出现对称性破缺现象，到目前为止，多尾迹的相互作用研究基本都是针对是阻力型尾迹的。图5给出了两个这样的例子，它们分别是并列圆柱[5]以及三个圆柱组成的圆柱群[6]的尾迹相互作用所形成的复杂流场。

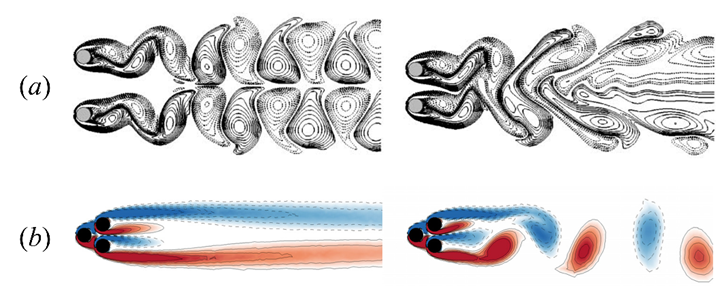
图5 多物体平行尾迹相互作用形成的复杂流场：(a) 并列圆柱的尾迹；(b) 三圆柱群的尾迹（图片来源：参考文献[5][6]）

张星研究员团队的研究针对仿水母式推进（即图6所示的反相对摆翼）产生的推力型尾迹[7]。在图6中，蓝色实线表示反相对摆翼，它们关于点划线所示的对称线（Line of symmetry）对称，其他的符号意义则分别是：d为间距， L为弦长，P₁和P₂为支点位置，L₀为前端到支点的距离，θ0为平衡张角，2A_θ为角振幅。这个高度简化的物理模型是受一些游动或飞行生物的启发而得到的：如推进的水母、并排游动的鱼、合拢-打开的昆虫双翅（参见图1）。显然，它的几何外形以及运动形式具有镜面反射对称性。先期的研究表明，在一定条件下，反相对摆翼的尾迹会出现自发的对称性破缺，进而影响其悬停稳定性和推进性能 [8][9]。但是，对于尾迹发生对称性破缺的临界条件和物理机制，人们目前尚不了解，因而该团队采用基于N-S方程的直接数值模拟（DNS）和Floquet稳定性分析相结合的方法展开了分析研究，以期揭示无来流条件下（即模型在流体中悬停时）反相对摆翼的尾迹发生对称破缺的物理机理。

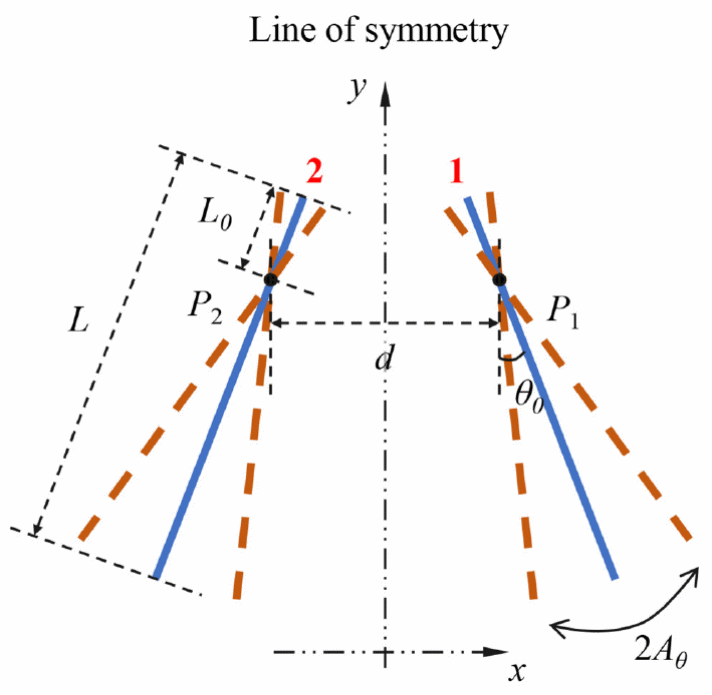
图6 仿水母式推进（反相对摆翼）的简化物理模型示意（图片来源：参考文献[7]）

首先，从DNS的结果可以看出，在“间距比”（即间距与弦长之比g = d/L）和“雷诺数 (Re)”组成的二维参数空间里，存在稳定性特性不同的6个区域（如图7所示）。在较低雷诺数下 (I区)，尾迹总能保持左右对称性。当超过某个临界雷诺数时，尾迹就会发生对称破缺。这个临界雷诺数的大小与间距比有关。在不同的间距比和雷诺数下，不稳定的尾迹可能分别表现出以下五种行为：（1）二次涡街重组（II区）；（2）涡对并后的二次涡街重组（III区）；（3）倾斜涡街（IV区）；（4）尾迹失稳后恢复对称性（V区）；（5）两股同相摆动涡街（VI区）。图7中的A，B，C，D为稳定区-不稳定区分界线上不同分段的分界点。

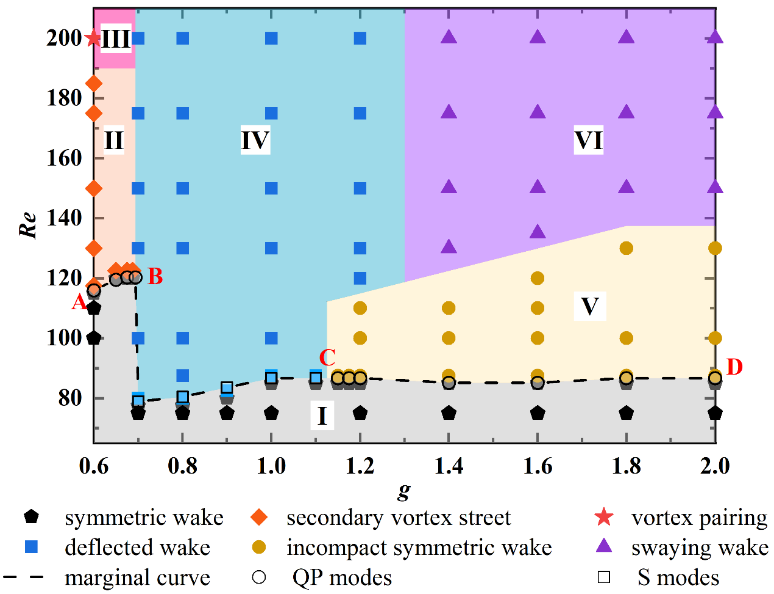
图7 参数空间 (g, Re) 上的尾迹类型分布。I：稳定对称尾迹；II：二次涡街；III：涡对并后二次涡街； IV：倾斜涡街； V：对称性可恢复尾迹； VI：两股同相摆动涡街（图片来源：参考文献[7]）

这项研究还有一个非常有趣的发现：尾迹的对称破缺对于平均推力的影响和尾迹的类型有关联。如果尾迹由对称涡街转变为倾斜涡街（即由I区跨越到IV区），平均推力会显著增加。而其它类型的尾迹对称破缺（如II区、V区和VI区）则不会引起平均推力的显著改变。这个发现对于仿生飞行器和水下航行器的设计有一定的指导意义。

Floquet稳定性分析的结果能够很好地预测图7中的稳定区-不稳定区分界线位置，并能对不同类型尾迹的演化过程给出合理解释。图8 - 10分别展示了三种不同类型的不稳定尾迹的Floquet分析结果。它们分别对应于II 区、IV 区和VI 区。由图可见，对于这三种不稳定尾迹，对称破缺都是由一个反对称的Floquet模态失稳所导致的。这里请注意：图8 - 10中显示的是涡量云图（“涡量”是指速度矢量的旋度在垂直于纸面方向的分量）。其中左右对称的速度剖面对应于一个左右反对称的涡量场；而左右反对称的速度剖面则对应于一个左右对称的涡量场。同时，我们还发现，如果将失稳的Floquet模态与基准流以某种方式叠加，就可以较准确地重构尾迹处于对称破缺最初阶段的DNS流场（请比较图8和图10中的d和e，以及图9中的c和d）。

由图8 -10还可以看出，三种不同类型尾迹的不稳定Floquet模态存在着明显的差异。图8和图10中的Floquet模态在远场有一个波长较大的大尺度结构；图8中的单列大尺度结构对应于涡街重组后形成的低频二次涡街；图10中的三列大尺度结构则对应于同相低频摆动的两股涡街。图9中的Floquet模态未见远场的大尺度结构，表明尾迹失稳后仅仅发生了一定程度的偏转，但并没有新的大尺度涡结构出现。Floquet模态在形态上的差异可能导致不同类型的对称破缺对推进性能的影响强弱不同。

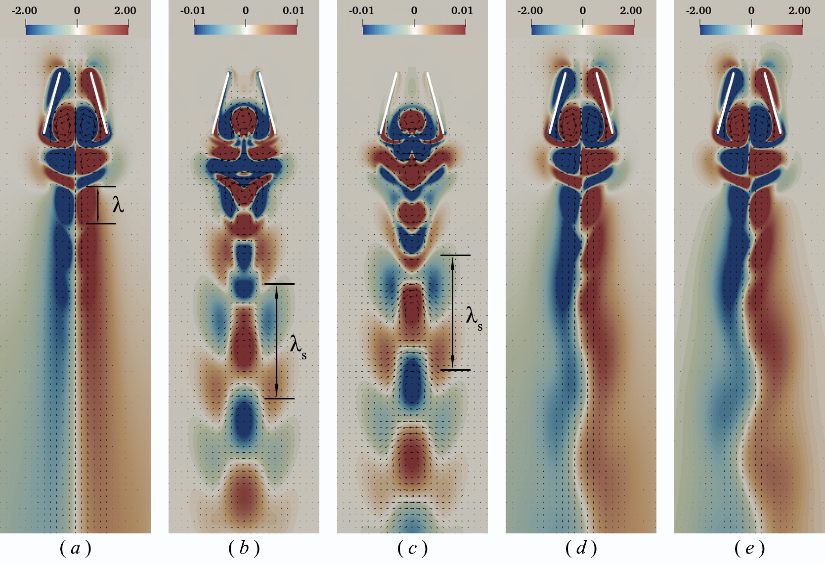
图8 不稳定区域II区算例的涡量图： (a) 基本流；(b) 不稳定Floquet模态的实部;(c)不稳定Floquet模态的虚部；(d) 基本流与Floquet模态的叠加；(e) DNS结果（图片来源：参考文献[7]）

图9 不稳定区域IV区算例的涡量图：(a) 基本流；(b) 不稳定Floquet模态（为实数）；(c) 基本流与Floquet模态的叠加；(d) DNS结果（图片来源：参考文献[7]）

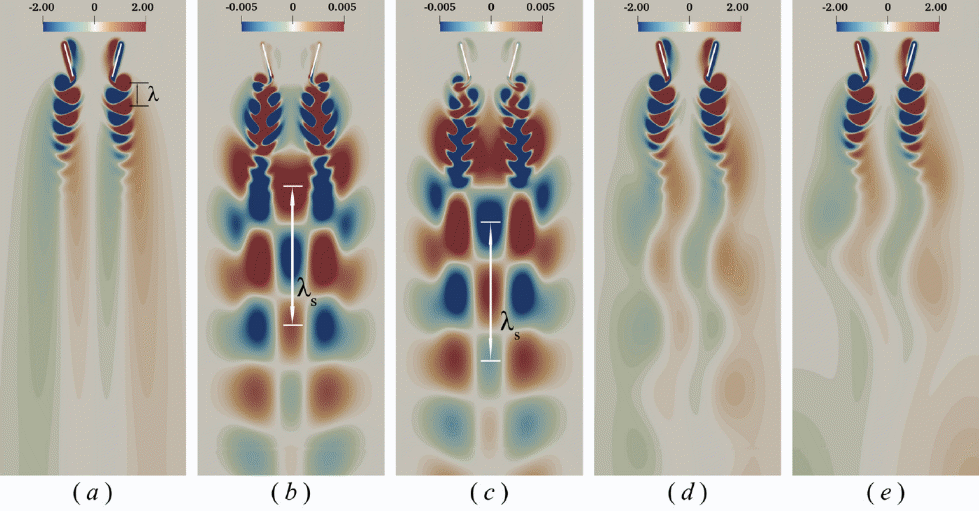
图10 不稳定区域VI区算例的涡量图：(a) 基本流；(b) 不稳定Floquet模态的实部；(c) 不稳定Floquet模态的虚部；(d) 基本流与Floquet模态的叠加；(e) DNS结果（图片来源：参考文献[7]）

因为篇幅的原因，这里没有展示III区和V区的情况。这两者的Floquet稳定性分析结果与II区的比较类似，但是它们的DNS结果和II区的则存在一些区别。III区的尾迹在发生对称破缺之前，还经历了一个“涡对并”的流动失稳过程（这个过程尾迹始终保持左右对称性）。V区的尾迹在发生对称破缺后，重组后形成的二次涡街未能长期维持下去，而是很快被耗散掉，其结果是尾迹的左右对称性最终得以重新恢复。

综上所述，这项研究工作揭示了仿水母式推进的尾迹发生对称破缺的关键物理机制。在今后的工作中，支点位置、平衡张角以及摆动角振幅对尾迹对称破缺的影响是值得进一步关注的问题。此外，如何利用主动流动控制来抑制或者促发尾迹的对称破缺，也是非常有意义的研究方向。

参考文献

[1] Jones K D, Dohring C M, Platzer M F. Experimental and Computational Investigation of the Knoller-Betz Effect [J]. AIAA Journal, 1998, 36: 1240-1246

[2] Zebib A. Stability of viscous flow past a circular cylinder [J]. Journal of Engineering Mathematics, 1987, 21: 155-165

[3] Barkley D. Linear analysis of the cylinder wake mean flow [J]. Europhysics Letters (EPL), 2006, 75: 750-756

[4] Jallas D, Marquet O, Fabre D. Linear and nonlinear perturbation analysis of the symmetry breaking in time-periodic propulsive wakes　[J]. Physical Review E, 2017, 95: 063111

[5] Kang S. Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers [J]. Physics of Fluids, 2003, 15: 2486-2498

[6] Cornejo Maceda G Y, Li Y, Lusseyran F, et al. Stabilization of the fluidic pinball with gradient-enriched machine learning control [J]. Journal of Fluid Mechanics, 2021, 917: A42

[7] Zhang Z, Zhang X. Instability mechanisms of symmetry breaking in the wakes of two anti-phase pitching foils at zero free-stream velocity [J]. Physics of Fluids, 2024, 36: 043610

[8] Zhang X, He G, Wang S, Zhang X. Locomotion of a bioinspired flyer powered by one pair of pitching foils [J]. Physical Review Fluids 2018, 3: 013102

[9] Gungor A, Khalid M S U, Hemmati A. Classification of vortex patterns of oscillating foils in side-by-side configurations [J]. Journal of Fluid Mechanics, 2022, 951: A73