北京大学力学系唐少强教授研究组在《Computational Methods in Applied Mechanics and Engineering》上发表了题为“虚拟聚类分析方法中参考材料强度的自适应选择”的研究论文，第一作者是该组的博士生朱熙同学。

　　数值均匀化是材料多尺度计算的重要方面，目的在于通过数值计算得到基于微观单元（如代表性体积单元）组成成分与结构的平均应力-应变关系，提供给宏观计算以实现准确的力学模拟。注意到给定平均应力（或应变）并不足以确定唯一的微观力学响应，在很大程度上还要看加载方式，人们通常采用周期边界条件。

　　该课题组之前提出虚拟聚类分析方法，通过聚类大大降低自由度和计算复杂度，再通过对与控制方程等价的积分方程离散化得到准确的代数系统，该积分方程涉及一个均匀线弹性参考材料。本研究发现，加载取决于参考材料的模量；对于弹性夹杂问题，微观单元的平均响应基本上不受参考材料的影响；但对于更复杂的问题，如弹塑性本构，加载方式会严重影响均匀化结果。进一步分析表明，参考材料的泊松比基本不影响加载，杨氏模量则起到举足轻重的作用。在此基础上，该文提出了恰当杨氏模量的判据，并给出了一个自适应选择恰当杨氏模量的数值方案。对于两种不同本构的弹塑性夹杂算例，通过与应力边界条件下的有限元数值模拟比较，验证了上述判据和自适应选择方案是有效的。该论文工作为进一步开展高效准确的数值均匀化和多尺度模拟提供了基础。

　　该论文得到了国家自然科学基金基础科学中心项目（基金号 11988102）的支持。论文链接：

　　https://www.sciencedirect.com/science/article/pii/S0045782520308069。

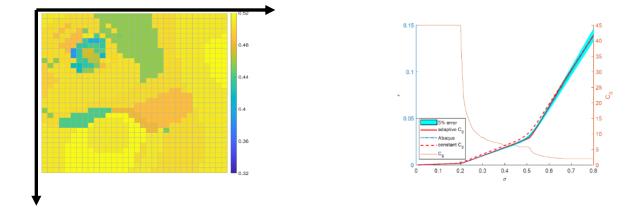
图10. 左图显示了夹杂问题在一个表面上的应力分布，它并不是均匀的；右图显示了采用本文方案得到的数值均匀化结果，以及加载过程中自动选择的参考材料杨氏模量。