近期，《Phys. Fluids》刊登了北京大学陈十一教授科研团队肖左利等人关于可压缩湍流时间不可逆性的研究工作。论文题目为《不同惯性的粒子映射的可压缩湍流时间不可逆性研究》（On the time irreversibility of compressible turbulence reflected by particles of various inertias）。该工作基于朗格朗日观点，通过分析粒子运动的功率标度律探讨湍流不可逆特性的可压缩效应和粒子惯性效应。

　　湍流是远离平衡态系统的典范。湍流的非平衡不可逆特征在湍流非线性动力学中扮演着至关重要的角色。肖左利等人基于示踪粒子和惯性粒子的拉格朗日追踪，研究了湍流可压缩性对不可逆性质的影响规律和机理。可压缩湍流的不可逆性可以通过颗粒与流场中的涡结构和激波结构的相互作用过程加以解释。图8所示为高马赫数湍流（Mt=1.01）中不同惯性的粒子在涡结构附近运动（a）或穿过激波运动（b）时半个大涡翻转时间内的运动轨迹，并由各自的瞬时功率染色。可以发现，较小惯性粒子的轨迹在遇到这些流动结构时比较大惯性颗粒具有更大的曲率，原因是小惯性粒子更倾向于压缩区域或涡核位置。实际上，粒子的瞬时功率在涡旋主导区域和应变主导区域都倾向于为负值。从压缩性影响看，在强压缩区粒子更倾向于获得负功率。在强可压缩湍流中，激波的出现使得更多的湍动能转化为内能，从而加剧了湍流的不可逆性。在弱可压缩湍流中，对示踪粒子来说由“flight-crash”现象引起的湍流不可逆主要发生在涡旋主导区，而对惯性颗粒来说则主要发生在应变主导区。

　　以上研究获得国家自然科学基金基础科学中心项目“非线性力学的多尺度问题研究” (基金号11988102) 资助。 论文链接：doi.org/10.1063/5.0041210。

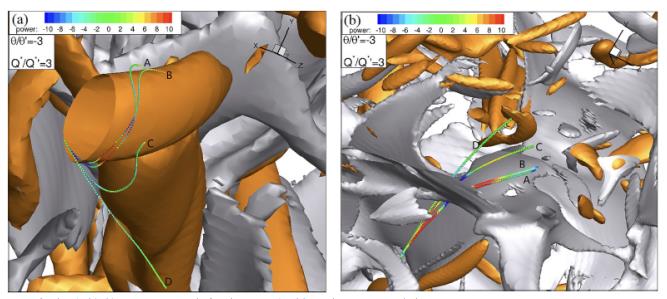
图8：湍流马赫数Mt=1.01流场中不同惯性颗粒（A:示踪粒子，B:St=0.1，C:St=1.0, D:St=5.0）遇到涡结构（a）和激波结构（b）时的运动轨迹。所有颗粒的初始位置相同，每个颗粒的迹线由瞬时功率进行染色。