近期，国际力学权威期刊《J. Mech. Phys.Solids》刊登了中国科学院力学研究所魏宇杰研究员科研团队在偏折裂纹尖端应力场的求解方面的研究进展。论文题目是《偏折裂纹尖端弹性应力场的解析解》。

　　裂纹偏折是工程实践中无法避免的力学现象，是断裂力学经典问题之一。裂纹可能由于动态裂纹扩展、结构非均匀性、局部应力状态变化等因素导致偏折。裂纹偏折不仅在安全设计方面有很大指导意义，在能源开采领域的价值也在日益凸显，在飞速发展的水力压裂领域有着广阔的应用前景。

　　经过多年攻关，团队采用Schwartz-Christoffel变换z=ω(ζ)，将复平面z上的偏折裂纹映射到复平面ζ上的单位圆上，使得边界值问题求解成为可能，进一步通过应用Muskhelishvili方法，求解获得了偏折裂纹的应力函数，以此为基础求解获得了任意几何尺寸的偏折裂纹尖端应力场，揭示了裂纹形状与裂纹应力场之间的关系（见图15理论与数值结果对照）。该小组的方法突破了偏折裂纹的长度限制，建立了任意长度偏折裂纹尖端应力场弹性解的通用求解方案。

　　以此为基础，可以相应地求解裂纹尖端的应力强度因子及应变能释放率，并以此建立了基于最大应变能释放率准则的偏折裂纹路径预测模型，该模型与有限元计算结果吻合良好。该方法同时可推广至多次裂纹偏折的弹性场求解。该研究成果为裂纹偏折行为和裂纹网络的形成机制提供了基础工具。

　　中科院力学所博士研究生刘卓尔为论文第一作者，魏宇杰研究员为论文通讯作者。以上研究获得国家自然科学基金基础科学中心项目“非线性力学的多尺度问题研究” (基金号11988102) 资助。论文链接：

　　https://doi.org/10.1016/j.jmps.2021.104619。

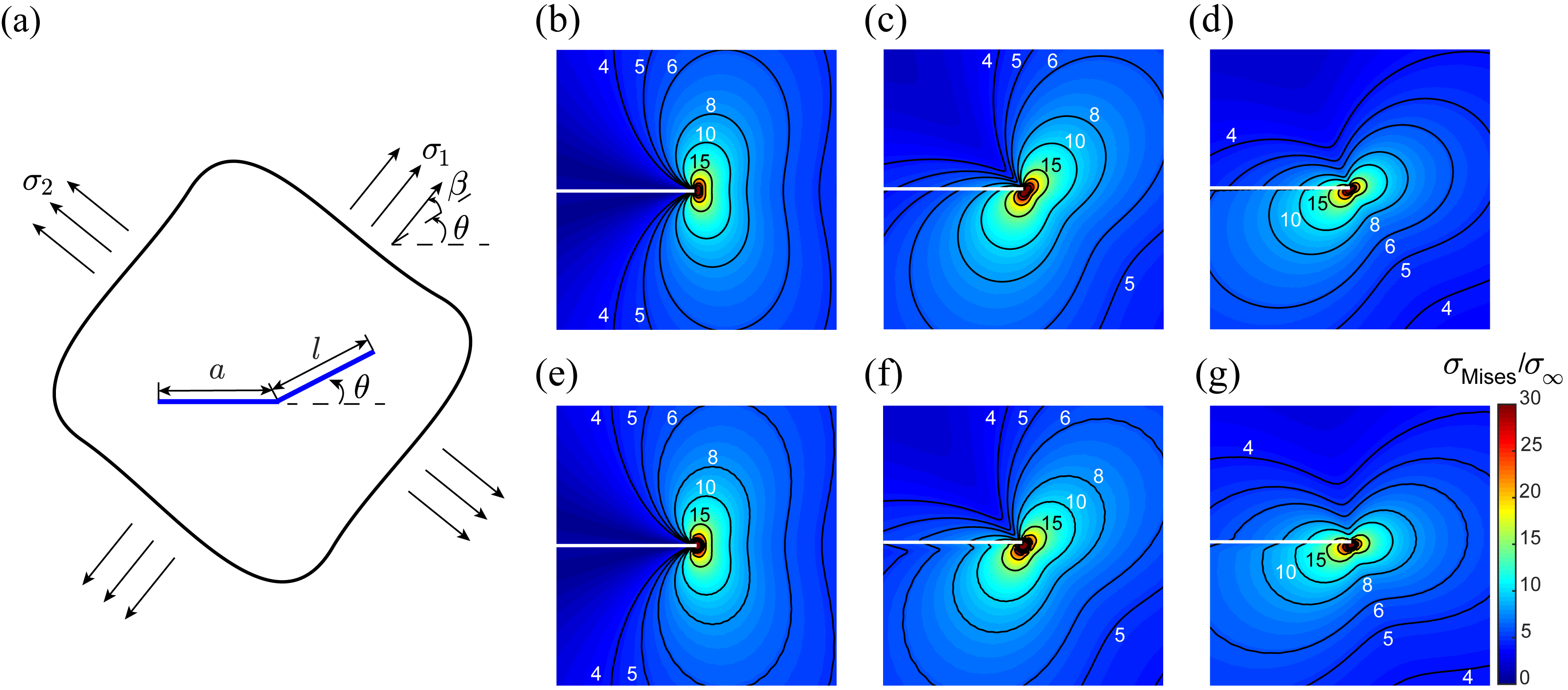
图15: 二维裂纹偏折问题的几何及加载参数、经过Schwartz-Christoffel变换后两个复平面间的映射关系（平面上的点分别对应平面上的点）以及单轴加载下不同转折角对应的裂纹尖端应力场（这里取）。其中(b)-(d)为本研究给出的解析弹性场von Mises应力（分别对应于），(e)-(g)为对应的有限元计算结果；为便于观察，图片经过旋转使得偏折裂纹部分沿水平方向。