编者按：力学研究所流固耦合系统力学重点实验室的“深部资源与环境力学”研究团队以深海采矿为背景，在粗颗粒管道内流的建模和流动特性分析方面开展了研究并取得了进展。本刊特此发布张岩等撰写的文章，介绍他们在深海矿产资源开发方面的工作，以飨读者。

为开发深海矿产资源做贡献

张岩 张旭辉 鲁晓兵

　　 我国的“十四五”规划和2035 年远景目标纲要强调：瞄准深地深海等前沿领域实施具有前瞻性、战略性的科学技术研究。因此，开发深海矿产资源成为必然选择。深海矿产资源开发涉及多个过程，我们力学工作者可针对其中的关键力学问题，以理论分析、数值计算和试验研究为手段，开展复杂海洋环境下深海采矿系统的可靠性研究。 

　　“管道提升系统”是目前公认的深海矿产资源最具应用前景的一种开采方式，图1是这种管道提升系统的示意图。大家可以看到，采矿车在海底做扫掠式运动，采集海底矿石；矿石粉碎后，经输送软管输运至储料仓；最后，再由垂直的输送硬管提升到水面采集船上。而在这个垂直硬管中，矿石物料则是凭借水力输送的。水力输送是用压力水流作载体，以一定速度向上运送矿石颗粒的输送方式。动力源来源于安装在输送硬管上的多级离心泵，依靠离心泵的离心力带动管道内的海水运动，海水运动的提升力进而携带矿石颗粒运移。图2示出水力输送过程中不同时刻管道内的矿石颗粒提升过程，这是一个数值模拟的结果。相传埃及金字塔的巨石也是依靠水力提升到达顶部的（图3）。 

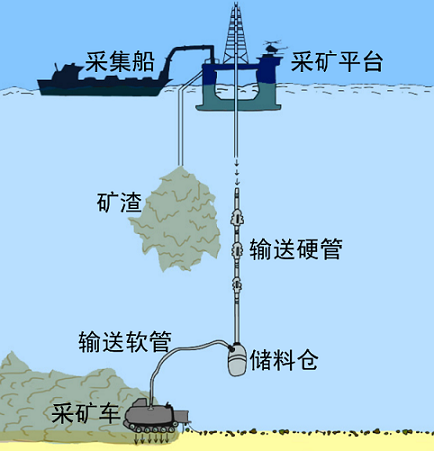
图1 管道提升系统示意图（来源daily.jstor.org/the-potential-pros-and-cons-of-seabed-mining）

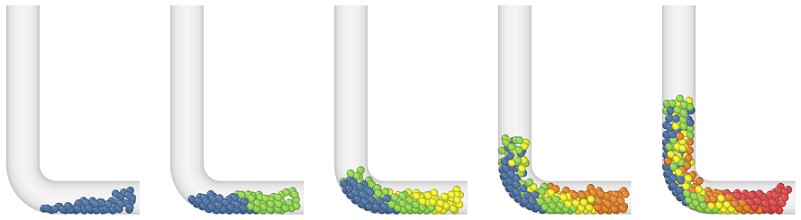
图2 水力输送过程数值模拟（E. A. Schnorr Filho, 2022, Powder Technology）

图3 金字塔建造过程巨石水力提升动图（来源： baijiahao.baidu.com/s?id=1684923918421603144&wfr=spider&for=pc）

　　所以，管道提升系统如何实现水力高效安全输送便是深海矿产资源开发技术的关键问题。因为在管道里的水体携带着碎矿石提升，就是流体力学所定义的一个固-液多相流体系，其中固相（也叫离散相）是矿石颗粒，液相（也叫连续相）是海水。对于深海采矿应用场景而言，固相中有许多粗大的块石，颗粒的含量甚高且尺寸大小不匀，所以这种输送过程具有“粗颗粒”、“高浓度”、“宽级配”等特征。在实际水力输送过程中，颗粒运动特征对实际工程的作业效率会产生重要影响。此外，实际开采中需要满足粗细颗粒混合和规模化连续输送（不发生流动堵塞）的作业要求，如何确保稳定输送也是对科学工作者的挑战。因此，掌握管道中含粗颗粒固-液两相介质的运动特征、流动阻力及稳定输送规律是优化开采方案的关键依据。 

　　目前，研究人员对这类多相流动规律的研究还不够深入系统，但它又是提升输送效率与保障输送安全的理论基础。中科院力学所流固耦合系统力学重点实验室的“深部资源与环境力学”研究团队以深海采矿为背景，在粗颗粒管道内流的建模和流动特性分析方面开展了研究并取得了进展。 

　　在流体力学里，常常采用欧拉-拉格朗日方法来计算固-液两相流的运动特性。对于连续相（海水），应用欧拉法（即研究流场中某一点处的运动特性）；而对于离散相（颗粒），则应用拉格朗日法（即研究流场中某一个质点微团的运动特性）。但是，当存在粗颗粒时，常规欧拉-拉格朗日方法会出现颗粒相分数过大、固液相间插值方法不适用等问题，导致数值模拟结果不准确或者计算发散而失败。这里的“相分数”是指颗粒的体积分数，即颗粒的体积在整个体系里所占的比例。 

　　目前欧拉-拉格朗日方法中使用最广泛的颗粒体积分数计算方法是颗粒中心法，它是将单个流体网格内的所有颗粒体积相加然后除以网格体积。这种平均化方法的物理意义明确，实现方便且求解速度快，但是它在粗颗粒存在时就不适用了，因为可能出现相分数大于1的非物理情况。因为颗粒粗大时，它的质心在网格内但有一部分体积会落在网格外。此外，由于颗粒采用拉格朗日方法追踪，计算颗粒在流体中运动时需要获得颗粒中心（这里，假设颗粒为球形）位置处的连续相场量（如速度、压力、密度等），以计算颗粒的受力状况。在通常情况下，连续相场量都是存储在网格中心点处的，而颗粒在运动时其中心点与网格中心点一般不重合，因此需要将网格单元中心点场量插值到颗粒中心点处。常见处理方式有两种：第一种是超近似方法，即令颗粒中心点处的连续相场量等于其所在网格单元的中心点值。第二种是采用网格节点插值的方法，根据颗粒中心点与其所在网格单元节点的距离作为权重，将网格节点量插值到颗粒中心点处。但是，这两种方法都不适用于粗颗粒情况，因为粗颗粒会占据多个网格，它的中心点处的连续相场量就和颗粒所占网格数量相关。 

　　针对常规欧拉-拉格朗日方法不适用于粗颗粒运动表征的问题，研究团队提出了一个修正模型。首先，他们提出了针对单个粗颗粒的虚拟质量分布函数法，用以求解粗颗粒相分数场。具体的实现思路是：将具有真实质量分布函数M_T(x)的颗粒扩大为一个具有虚拟质量分布函数M_V(x)的虚拟大颗粒，重构其质量分布，并保证守恒性、有界性和光滑性（如图 4）。这里，“有界性”是指虚拟质量分布函数的积分收敛且有界；“守恒性”是指重构前后的颗粒总质量不变；“光滑性”是指虚拟质量分布函数是光滑且可导的函数，以防止在颗粒表面出现间断造成数值不稳定。在虚拟质量分布函数的基础上，通过将虚拟质量分布函数在流场全域上积分得到粗颗粒的相分数场。此方法的优点在于程序实现容易，求解速度快且适用于稠密相问题。 

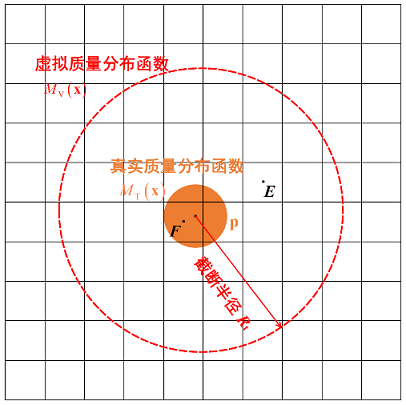
图4 虚拟质量分布函数示意图

　　随后，他们提出了基于粗颗粒尺寸的欧拉-拉格朗日场的一种改进的插值方法。因为在离散相求解时颗粒位置与流场数据存储点位置不重合，而且颗粒占据数个流场网格区域，所以需要考虑颗粒尺寸的影响。因此，通过将颗粒占据的流场网格单元都考虑进来进行权重插值，权重计算根据流场位置与颗粒中心位置的距离计算。这种插值方法显著提高了计算的准确性。 

　　对于这个针对含有大量粗颗粒情况所发展的修正模型，研究团队采用气-固流化床作为算例进行验证，并与相关的计算和实验结果进行了对比。图5（a）为算例中流化床的设置，给出了床体的长L宽W高H，颗粒的密度ρ和直径d以及进气速度U。图5（b）（c）则分别给出粗颗粒相分数和颗粒垂直速度的计算结果。通过对比可以看出，颗粒中心方法计算得到的粗颗粒相分数离散性较大，而虚拟质量分布函数法计算结果则更平滑，同时与多重网格网格计算结果基本相同（如图5（b）所示）。此外，与其他插值方法相比，权重插值方法显然计算结果更精确（如图5（c）所示）。 

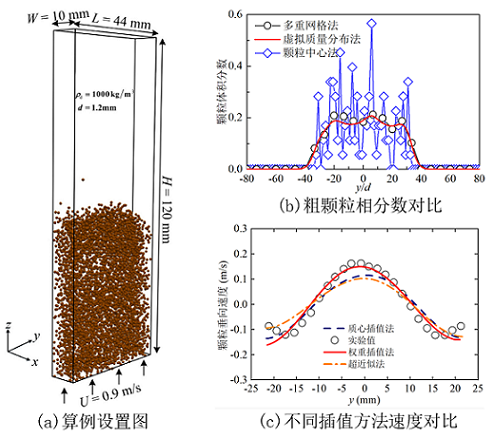
图5 气-固流化床算例计算结果对比

　　最后，研究团队基于他们提出并经过验证的修正模型，进行了实际尺寸管道内的水力输送过程数值模拟。他们首先分析了宽级配颗粒在管道中的运动特性，获得了颗粒群（这里显示的是混合粒径的颗粒群，既有粗也有细）在垂直管道中的分布形态（参见图6）。 

图6 颗粒在管道中的分布形态

　　从图6中不难发现，颗粒群在输送过程中呈现明显的疏密流动形态，这种形态产生的原因主要是颗粒滞留和颗粒分离。这里，“颗粒滞留”是指颗粒与海水之间有速度滑移（“滑移”指两相的运动速度有差异）而导致颗粒在管道中局部颗粒浓度显著增加的现象，粗颗粒存在时这种现象会更明显。“颗粒分离”是指粗细颗粒混合运动时细颗粒的运动速度大于粗颗粒的运动速度而导致的颗粒分层现象。研究团队分别分析了颗粒滞留和颗粒分离效应的强弱，发现宽级配特征下颗粒的分离效应对颗粒局部浓度有显著影响，而颗粒滞留效应受输送速度的影响最大，从而给出了粗颗粒滞留与细颗粒分离引起疏密流动形态的形成机制。 

　　对于上述的颗粒分离现象，研究团队还基于自建的实验装置开展了试验和相应的计算，并进行了对比（参见图7，8）。图7给出了自建实验装置的结构，图8对比了数值模拟和实验中两种尺寸（直径6 mm和13 mm）颗粒在不同输送流量（Volume flow rates）时颗粒分层高度（Height）的变化。不难看出，计算和实验结果基本符合。 

图7 垂直管道固液两相介质水力输送实验装置及测量模块示意（图片来源：作者拍摄）

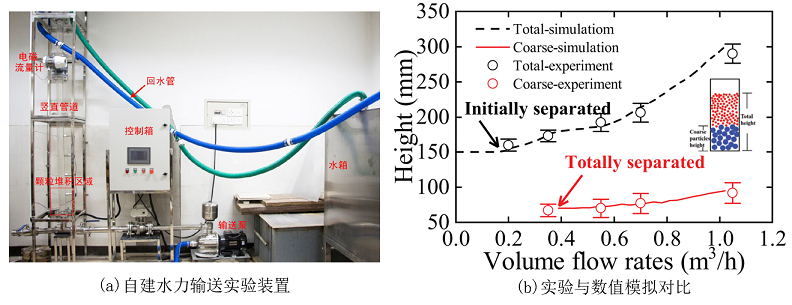
图8 基于自建实验装置的颗粒分离实验对比

　　研究团队的模拟结果还表明，管道中部处的颗粒浓度随着输送速度的增大而减小。当输送速度（Water inlet velocity）较小时（1-2 m/s），该局部处的颗粒浓度（Particle concentration）降低较快，而输送速度较大时（3-5 m/s），该局部处的颗粒浓度变化很小（参见图9）。这样，就给出了实际输送合理的输送速度取值范围建议。分析这一现象产生的原因，他们发现当输送速度为2-3 m/s时，流型从疏密流动向均匀流动转变，流型转变导致颗粒的运动形态发生变化。而流型转变的原因，初步分析是由于颗粒碰撞效应和水动力效应的大小发生变化，在疏密流动中颗粒碰撞效应占主导，而在均匀流动中水动力效应占主导。这两种效应决定了固相和液相两相之间动量交换的强弱。对这一现象，研究团队后续拟进行更深入的分析。 

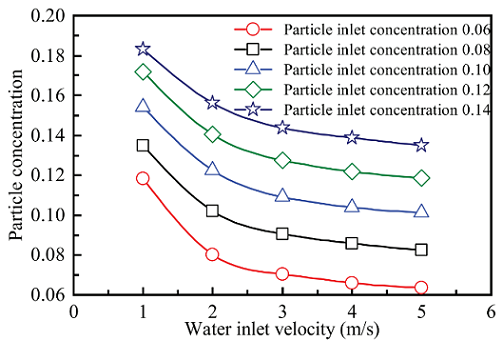
图9 颗粒浓度随着输送速度的变化关系

　　最后还要强调的是，研究团队基于量纲分析方法给出了两相流动过程的主要控制无量纲参数：输送雷诺数、弗劳德数、颗粒尺寸与管道直径比、密度比等。综合数值模拟数据并参考前人研究的结果，他们给出了管道内局部参数以及阻力损失计算的预测无量纲关系式。如图10（a）所示，其中的两条曲线分别是两个不同d/D值下（这里，d为颗粒直径，D为管道直径）的无量纲预测关系式，通过与实验数据对比，验证了无量纲预测关系式的有效性。在实际深海采矿中，要满足商业化开采的要求，每天的矿石输送量需要达到数万吨量级，因此工程界关心输送阻力和管道的输送能力（即单位时间输送量）。基于无量纲关系式，他们分析了单位时间颗粒输送量（Amount of particles lifted）的变化。如图10（b）所示，随着颗粒输送体积浓度（Particle inlet concentration）的增加（变化范围0.05-0.2），颗粒单位时间的输送量先增大后减小，在输送浓度0.1时颗粒输送量最大，因此他们建议工程中设置颗粒输送浓度为0.1比较合适。此外，基于数值模拟结果，他们还给出了水力输送过程管道水头损失的预测关系式，基于此关系式可以计算长距离管道输送过程中输送泵所需扬程的大小。总之，研究团队的研究成果为长距离管道输送的流动保障提供了理论支撑。 

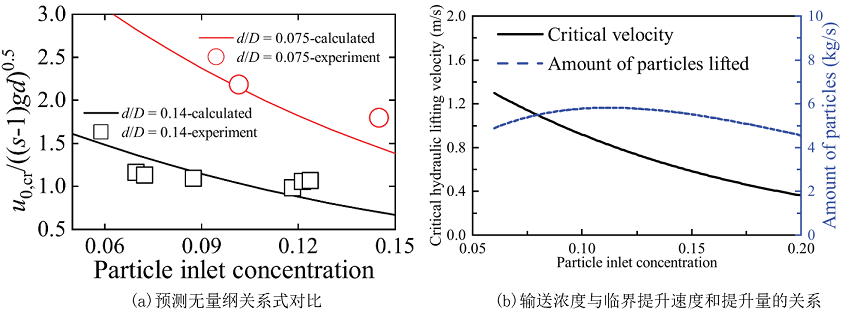
图10 预测无量纲关系式的实验数据验证 

　　相关的研究成果发表于流体力学一类重要期刊Physics of Fluids（POF 2021, 33: 113307；POF 2022, 34: 033305），并被期刊评选为Editor’s pick文章。当然，中科院力学所流固耦合系统力学重点实验室的“深部资源与环境力学”研究团队会继续努力，为我国深海矿产资源的开发做出更多的贡献。 

参考文献 

　　[1] Zhang Y, Lu X, Zhang X. An optimized Eulerian–Lagrangian method for two-phase flow with coarse particles: Implementation in open-source field operation and manipulation, verification, and validation [J]. Physics of Fluids, 2021, 33(11): 113307. 

　　[2] Zhang Y, Lu X, Zhang X. Numerical simulation on transportation behavior of dense coarse particles in vertical pipe with an optimized Eulerian-Lagrangian method [J]. Physics of Fluids, 2022, 34(3): 033305.