编者按：中国科学院力学研究所高温气体动力学国家重点实验室的可压缩湍流与转捩研究团队，近年来在旋转湍流与螺旋度的研究方面取得了很好的进展，有多篇文章在Journal of Fluid Mechanics等国际顶级期刊上发表。本刊特此发布于长平介绍相关进展的文章，以飨读者。  

 

湍流、旋转湍流与螺旋度——兼谈旋转湍流中能量与螺旋度的尺度输运效应

于长平

　　湍流是自然界和航空航天等工程领域中普遍存在的一种流体运动状态。流体的另一种流动状态则是层流。当流体的流速很小时，流体分层流动，互不混合，称为层流，也称为稳流或片流；当流速增加到很大时，流线不再清楚可辨，流场中有许多小漩涡，相邻流层间不但有滑动还有混合，称为湍流，又称为乱流或紊流。1883年，英国科学家奥斯本 雷诺用玻璃管做试验（参见图1,2），区别出发生层流或湍流的条件。因此，流体力学中一个重要的无量纲参数就被命名为雷诺数Re= vd/ （其中 、v、 分别为流体的密度、速度和黏性系数，d是一个特征长度。例如流体流过管道时，d为管道的当量直径）。图3则给出了湍流形态的可视图像：雷诺把试验的流体染色，可以看到染上颜色的质点在层流时都沿着直线运动。当雷诺数超过某个临界值时，流体质点的运动轨迹变乱了，在时间和空间上都有脉动，并发生随机性的混合，这就是湍流。雷诺试验的完成与雷诺数的提出，对于流体力学的发展具有重要的贡献。 

图1 英国科学家奥斯本 雷诺（1842—1912）（图片来源：网络）

图2 著名的雷诺试验（图片来源：网络）

 

（a）层流  

（b）湍流  

图3 雷诺试验中展示的两种流体运动状态（图片来源：网络）

　　通过研究湍流，我们会加深对自然界中各种现象的理解与认识。例如，利用计算模型和数值方法，人们可以探讨龙卷风和飞行器绕流的结构（参见图4）。另外， 湍流的广泛出现也决定了其必然存在的广泛应用场景，例如减阻、提高流体机械的可靠性、控制发动机喘振等等。  

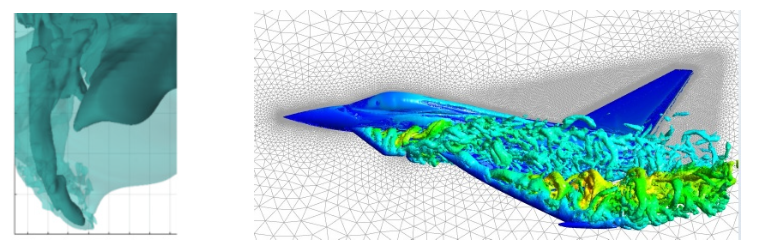
图4 左：龙卷风的模拟[1] 右：飞行器绕流的模拟（图片来源：网络）

　　当然，如果从数学的角度来看，流体运动的控制方程（Navier-Stokes 方程）是一个典型的非线性方程，所以湍流问题本质上是一个非线性问题。随着对湍流认识的加深，人们也加深了对一类非线性问题的认识。在湍流的基础研究中，研究者们很关注的一点是：多尺度效应及级串。这里的“尺度”是指湍流中旋转运动着的流体微团的大小，这些微团也被称之为“旋涡”。在湍流中包含着大大小小的旋涡，所以流动可以被分解为不同的尺度。它们之间存在着动量、能量等物理量的交换（力学家采用术语“输运”来描述这个交换过程）。所谓的“级串”可以被简单解释为能量或其他物理量在不同尺度之间的输运。英国科学家路易斯 弗莱 理查德森写于1922年的一首小诗最早给出了关于级串的抽象描述：“大旋涡育小旋涡以动能，小旋涡亦以此孕子女，生生世世以之更迭，终消于粘滞”（参见图5）。而“粘滞”则和流体的一个固有物性“粘性”（viscocity）相关，后者表示流体内部各微团或流层之间由于具有相对运动而产生内摩擦力以阻止流体做相对运动的性质。在湍流中，一般而言，能量由大尺度向小尺度输运，这通常被称为正向级串。反之，当能量由小尺度向大尺度输运时，则被称为反向级串。  

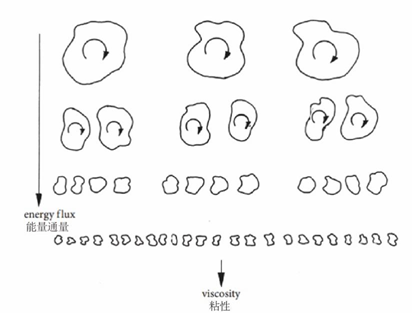
图5 湍流中能量级串[2]

　　这里应当指出的是：在不同的场景中，湍流的形态不尽相同。当流体在整体上进行旋转运动时，此时的湍流被称为旋转湍流。自然界的台风、气旋等就是典型的旋转湍流。而在工程应用中，传统的动力机械常常是通过旋转与压缩、膨胀等效应来进行机械功与内能、化学能之间的能量转换，这里往往也涉及到旋转湍流。目前人们对于旋转湍流的研究仍然主要停留在基础研究的层面。以旋转圆筒实验为例（参见图6左），研究者们将坐标系固定在旋转的圆筒之上，这是通过与圆筒同步旋转的相机来实现的。在这种坐标系变换下，圆筒旋转效应具体化为两种虚拟力：离心力与科氏力（参见图6右）。离心力使回转的流体微团远离它的旋转中心，而科氏力则描述旋转系中流体微团的惯性偏移。对于不可压缩流体而言，离心力的效应可以与压力作用合并进行研究，所以人们的研究重点放在了科氏力上面。这里介绍我们团队在这个领域的研究工作进展。  

 

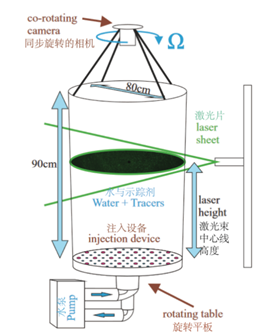
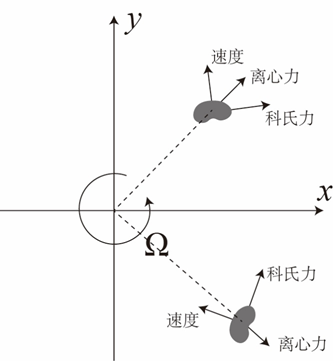
图6 左：旋转圆筒实验[3] 右：旋转系中的虚拟力示意图（图片来源：作者自制）

　　如前面提到的，自然界的台风、气旋等都是典型的旋转湍流，它们均是大气运动的展现。图7示出了西风带的非定常波动现象，由于地球自转导致的科氏力，形成了Rossby 波（参见图7左）和准 Keplerian 流动（参见图7右）。我们在此研究背景下考虑了科氏力的影响[4]。我们发现了非均匀旋转湍流新的标度、以及科氏力导致的空间输运效应。如图8所示，上、下半域在统计意义上是对称的。上半域显示了强旋涡结构，下半域显示了强度相对较弱的旋涡结构，蓝色、红色分别代表正、负涡量。这里的涡量是旋涡强度、方向的定量表征。我们发现，由（a）到（c），随着非均匀旋转效应的增强，能量由强旋转区域向弱旋转区域输运。这些结果不仅有助于强化对大气运动的认识，还可以指导同属于非均匀旋转流动类型的旋转机械的设计优化。  

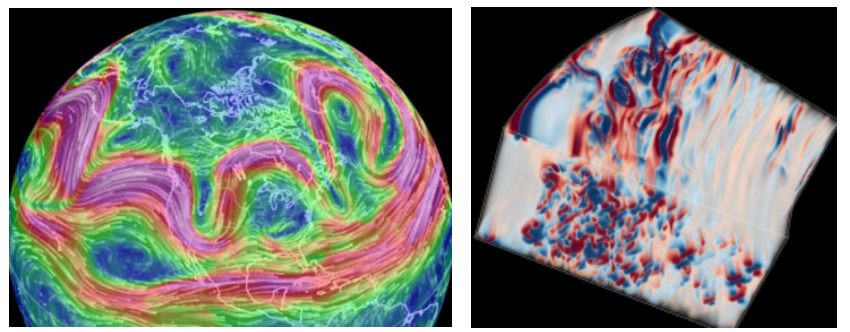
图7 左：大气中的Rossby波（图片来源：网络） 右：准Keplerian流动[5]  

　　  

 

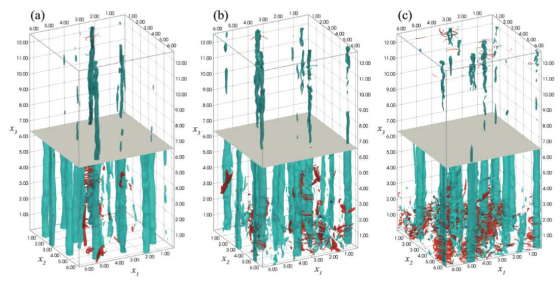
图8 非均匀旋转湍流结构：（a）均匀旋转；（b）弱非均匀旋转；（c）强非均匀旋转[4]  

　　大家知道，旋转会引入“手性”的不对称。在流体力学中，手性通常指代速度与涡量方向的一致性，一般通过螺旋度来衡量。这里的术语“涡量” (vorticity)是流体速度的旋度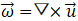，描述了流体中某点附近的局部旋转运动。螺旋度则被定义为速度与涡量的点积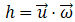：，但它是一种“伪标量”，即其值可以有正、负区别。在图9中，我们以红、黄、蓝三种颜色区分流场中的三条流线。如果有涡量时流线是旋曲的：若涡量方向向下则流线左旋，若涡量方向向上则流线右旋。关于螺旋度正负值的规定如下：当速度与涡量方向相反时，螺旋度为负；当涡量消失或涡量与速度垂直时，螺旋度为0；当涡量与螺旋度方向相同时，螺旋度为正。螺旋度的正负便表示为手性。 

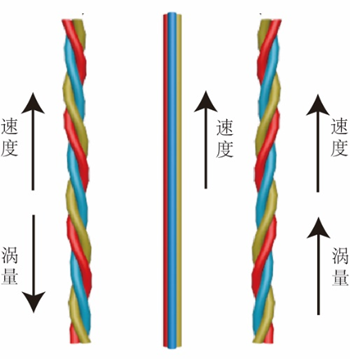
图9 三种螺旋度取值下的典型流线示意图。左：负螺旋度；中：无螺旋度；右：正螺旋度。（图片来源：作者自制）  

　　为了使大家有感性的理解，图10中展示了湍流结构的几种典型情况，它们分别是：（a）无螺旋度且无旋转;（b）无螺旋度而有旋转；（c）满螺旋度且有旋转。  

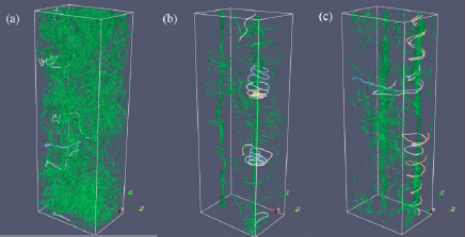
图10 旋转湍流的几种典型流动结构：（a）无螺旋度无旋转;（b）无螺旋度有旋转；（c）满螺旋度有旋转 [6]  

　　在此基础上，我们研究团队提出了螺旋度双通道级串理论等流动机制[7,8]，并且发展了一系列基于螺旋度的大涡模拟模型[9,10]，这类模型在旋转湍流等相关问题上具有较强的适用性。图11给出无旋转效应时螺旋度级串的双通道的图示。这里的双通道主要分别与旋涡的扭曲与拉伸作用相关。图中横坐标为尺度输运的强度，纵坐标为不同的尺度。图（a）所示的螺旋度级串第一通道表示旋涡扭曲作用占优的情况，此时能量向小尺度输运。而螺旋度级串的第二通道表示旋涡拉伸作用占优的情况，此时能量向大尺度输运。图12则给出了旋转湍流中的能量级串的分析结果。横坐标为尺度，纵坐标为能量的级串，正值代表正向能量级串，负值则相反。绿色的线代表了整体的能量级串，其他三种线型代表了对能量级串的分解。图中结果显示，旋转湍流中反向的能量级串随着螺旋度的引入被抑制。  

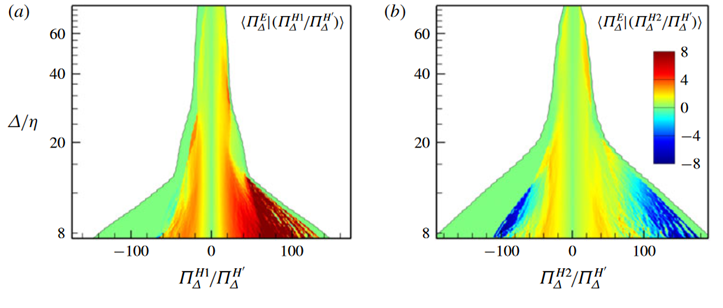
图11 无旋转效应时螺旋度级串的双通道：（a）螺旋度级串第一通道（b）螺旋度级串第二通道[7]

 

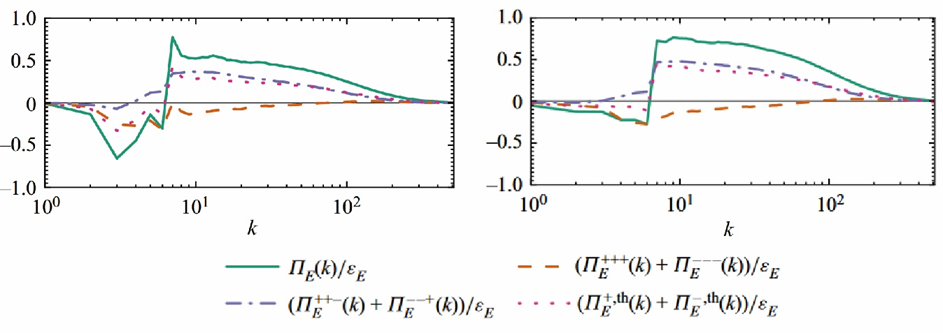
图12 旋转湍流的能量级串分解：左：无螺旋度有旋转；右：有螺旋度有旋转[6]  

　　我们的工作系统地分析了能量与螺旋度级串的守恒性与对称性，提出了螺旋度级串的新表达式，推导并证明了其与传统表达式的区别与联系。我们发现螺旋度会对旋转导致的能量反向级串产生明显抑制效应，这是该现象的首次发现。此外，通过对螺旋度输运的理论分析发现了螺旋度手性极化等现象的新物理机制。该工作不仅深化了螺旋度与旋转效应在湍流演化中的耦合作用理论，而且拓展了螺旋度尺度分析在复杂湍流研究中的应用。  

　　此外，我们还研究了流向旋转槽道湍流中的涡结构（参见图13）。这类流动最显著的特点在于流向旋转会引入展向二次流，即与主流方向垂直方向上的流动。这种二次流会在槽道中心区变号，被称为槽道中心的反向二次流。随着旋转加强，脉动流中也出现了大尺度准流向涡结构。弱旋转下，这种大尺度准流向涡实际与流向呈现一定倾角，如图13所示。但在强旋转下，这种涡结构则是基本与流向对齐的。  

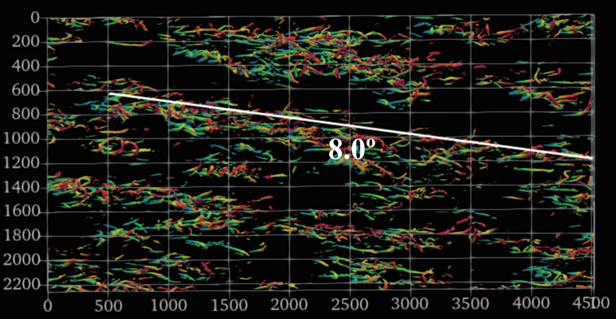
图13 流向旋转槽道的涡结构[11]  

　　另外，在槽道湍流中，旋转会破坏手性对称性，引入螺旋度。本课题组首次在这一流动中研究了螺旋度的分布特征（参见图14），给出了流向旋转槽道中的发卡涡结构，包括螺旋度和涡线分布。  

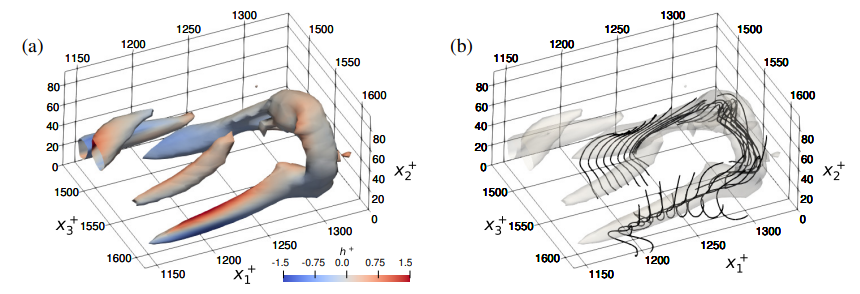
图14 流向旋转槽道中的发卡涡结构：（a）螺旋度分布；（b）涡线分布[12]  

　　在湍流基础研究与高精度数值模拟领域，螺旋度的相关研究主要集中在一般湍流及与其它物理效应耦合的湍流，如热对流、磁流体效应等。而在海洋数据方面，由于采样数据多为二维， 螺旋度的相关研究也十分罕见。我们课题组的研究填补了螺旋度与壁面流动耦合效应研究的空白，不仅给出了螺旋度的分布特征，还揭示了Reynolds数效应、级串等现象，从而将螺旋度研究进一步地向实际工程应用靠拢。  

　　  

参考文献  

　　[1] Yao D, Xue H, Yin J, et al. Investigation into the formation, structure, and evolution of an EF4 tornado in east china using a high-resolution numerical simulation[J]. Journal of Meteorological Research, 2018, 32: 157-171.  

　　[2] Davidson P A. Turbulence: an introduction for scientists and engineers[M]. Oxford university press, 2015.  

　　[3] Yarom E, Vardi Y, Sharon E. Experimental quantification of inverse energy cascade in deep rotating turbulence[J]. Physics of Fluids, 2013, 25(8): 085105.  

　　[4] Hu R, Li X, Yu C. Effects of the Coriolis force in inhomogeneous rotating turbulence[J]. Physics of Fluids, 2022, 34(3): 035108.  

　　[5] Shi L, Hof B, Rampp M, et al. Hydrodynamic turbulence in quasi-Keplerian rotating flows[J]. Physics of Fluids, 2017, 29(4): 044107.  

　　[6] Running Hu, Xinliang Li, Changping Yu. Transfers of energy and helicity in helical rotating turbulence, J. Fluid Mech. (2022), 946, A19   

　　[7] Zheng Yan, Xinliang Li, Changping Yu, Jianchun Wang and Shiyi Chen. Dual channels of helicity cascade in turbulent flows. J. Fluid Mech. (2020), 894, R2   

　　[8] Changping Yu, Running Hu, Zheng Yan, Xinliang Li. Helicity distributions and transfer in turbulent channel flows with streamwise rotation, J.Fluid Mech. (2022), 940, A18   

　　[9] Han Qi, Xinliang Li, Running Hu, Changping Yu. Quasi-dynamic subgrid-scale kinetic energy equation model for large-eddy simulation of compressible flows, J. Fluid Mech. (2022), 947, A22   

　　[10] Changping Yu, Zelong Yuan, Han Qi, Jianchun Wang, Xinliang Li, Shiyi Chen. Kinetic-energy-flux-constrained model using an artificial neural network for large-eddy simulation of compressible wall-bounded turbulence. J. Fluid Mech. (2022), 932, A23  

　　[11] Running Hu, Xinliang Li, Changping Yu. Multiscale dynamics in streamwise-rotating channel 2 turbulence, J. Fluid Mech. Under Review  

　　[12] Running Hu, Xinliang Li, Changping Yu. Effects of streamwise rotation on helicity and vortex in channel turbulence, J. Fluid Mech. Under Review